32位环境下VC/VS除法的8种汇编形态及传说中的MagicNumber

欢迎转载，转载请注明出处！原文地址

Follow me on GitHub ^_^

##

• 1. 8 / n 常数除变量
• 2. 有符号变量除正负2的幂
  • 正
    • 公式
    • 特征
    • 还原
  • 负
• 3. 无符号变量除正2的幂
• 4. 无符号变量除正非2的幂（且非7及其倍数）
  • 公式
  • 特征
  • 还原
  • 无符号变量除负非2的幂
• 5. 无符号变量除7
  • 公式
  • 特征
  • 还原
• 7. 有符号数除正非2的幂
  • nVar / 7
    • 指令分析
    • 公式
    • 特征
    • 还原
  • nVar / 5
    • 指令分析
    • 特征
  • nVar / 3
    • 指令分析
    • 特征
• 8. 有符号数除负非2的幂
  • nVar / -3
    • 指令分析
  • nVar / -5
  • nVar / -7

1. 8 / n 常数除变量

直接上除法指令

...
mov    eax, 8          // 8 / nVar
mov    esi, ds:printf
cdq
idiv    [esp+14h+nVar_4]
...

2. 有符号变量除正负2的幂

正

...
mov    eax, [esp+1Ch+nVar_4] // nVar / 8
cdq
and    edx, 7
add    eax, edx
sar    eax, 3
...

公式

向零取整：正数除法向下取整，负数除法向上取整；移位属于向下取整

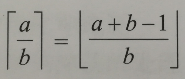
特征

mem -> nVar
c   -> 8
m   -> 3 -> 2^3 == 8

...
mov eax, mem       // 将数据移动到eax寄存器
cdq                // cdq符号位扩展到edx
and edx, c - 1     // and后正数edx结果为0，负数edx结果为c - 1
add eax, edx       // 最终，正数不变，负数 + (c-1)
sar eax, m         // 有符号右移替代除法
...

还原

不用在意变量为负数的情况，直接拿出移位数，转化为nVar / 2^m

负

...
mov    eax, [esp+0Ch+nVar_4]  // nVar_4 / -8
cdq
and    edx, 7
add    eax, edx
sar    eax, 3
neg    eax                    // 只多了个求补，相当于符号取反
...

3. 无符号变量除正2的幂

直接右移

...
mov    edi, [esp+24h+nArgc] ; nArgc / 16
mov    ecx, edi
shr    ecx, 4
...

4. 无符号变量除正非2的幂（且非7及其倍数）

mov    eax, 0AAAAAAABh // uArgc / 3
mul    edi
shr    edx, 1

公式

a为无符号正数，c为正数常量，n由编译器决定、越大误差越小，m就是传说中的MagicNumber（关于这个最后再议）

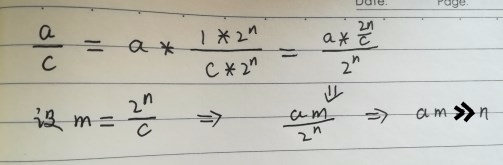
特征

M -> MagicNumber -> 0AAAAAAABh
n -> 移位数
N -> 再次移位数（如果mul的操作数为edi，则已经右移了32为，后面shr是再次移位，还原时需注意）

mov eax, M
mul reg/mem  // a * m
shr edx, N   // a * m >> 32+N -> a * m >> n

还原

m = 2^n / c => 2^n / m = c
以上面的uArgc / 3为例

• 首先拿到魔法数M->0AAAAAAABh
• 然后分析移位数n（mul操作数为edi，已经移了32位，因此n = 32 + N）-> 32 + 1 = 33
• 套用m / 2^n = c还原->2^33 / 0AAAAAAABh = c得到结果为非整数，向上取整后c =

无符号变量除负非2的幂

mov    eax, 40000001h   // uArgc / -3
mul    [esp+0Ch+uArgc]
shr    edx, 1Eh

和无符号变量除正非2的幂的特征一样（因为有无符号混除会被视为无符号数，在运算时uArgc / -3相当于uArgc / FFFFFFFDh）

所以反推回来的c值：无符号为：4294967293/FFFFFFFDh，有符号位：-3

5. 无符号变量除7

...
mov    ecx, [esp+0Ch+uArgc]  // uArgc / 7
mov    eax, 24924925h
mul    ecx
sub    ecx, edx
shr    ecx, 1
add    ecx, edx
shr    ecx, 2
...

公式

首先根据上面的汇编可以推出（假定24924925h为MagicNumber）：

• mul ecx这一句执行后ecx和eax相乘，结果在edx.eax，而直接拿出edx进行后面的运算，相当于将ecx和eax相乘的结果右移32位（除2^32）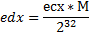

  

• sub ecx, edx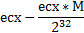

  

• shr ecx, 1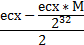

  

• add ecx, edx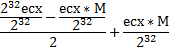

  

• shr ecx, 2

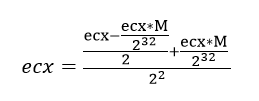
• 化简：

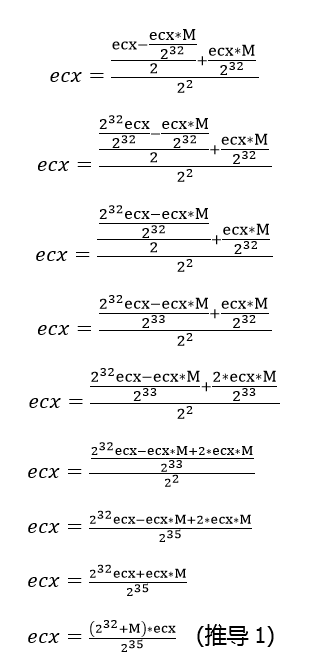
• 推导：

• 结论：经过上面的推导我们可以发现2^32 + M相当于MegicNumber发生了进位，最高位超出了32位，因此需要通过加上2^32来将MegicNumber还原成正确的值。而最终通过汇编代码表现的是上面那堆公式的反推过程，将复杂的公式反推至不会发生溢出的汇编代码

特征

mov    eax, imm
mul    reg
sub    reg, edx
shr    reg, 1
add    reg, edx
shr    reg, 2

还原

和前面无符号变量除正非2的幂的还原方式一样，只是这里的n为直接使用edx产生右移32位再加上后面两次右移的结果，而MagicNumber要加上溢出的最高位+100000000h：m = 2^n / c => 2^n / m = c

7. 有符号数除正非2的幂

nVar / 7

...
mov    ecx, [esp+0Ch+nVar_4]  // nVar_4 / 7
mov    eax, 92492493h
imul   ecx
add    edx, ecx               // 比无符号除正非2的幂多了这一条
sar    edx, 2
mov    ecx, edx               // 比无符号除正非2的幂多了这一条
shr    ecx, 1Fh               // 比无符号除正非2的幂多了这一条
add    edx, ecx               // 比无符号除正非2的幂多了这一条
...

指令分析

先来分析多的第一跳指令：add edx, ecx

• 发现nvar / 7的MagicNumber为92492493h（32位），很明显这个数的高位为1，且下面的指令是imul，说明MagicNumber被当作有符号数处理了；然而MagicNuber是个无符号数，这就产生了一个无符号数和有符号数相乘（将92492493h视为正数与有符号数nVar相乘）结果还要“正确”（不考虑溢出，因为这里的imul指令后面是单操作数，所以溢出的部分会存在edx中）的问题。

• 我们想要知道怎样才能保持结果是“正确”的，就必须先看“错误”的会是什么样：

  为简化公式，这里将32位的92492493h截断为16位的9249h，单操作数的imul指令的结果存放在16位寄存器dx.ax中

  • 上面发生“错误”的指令可以写成公式：nVar * 9249h，如果将9249h视为有符号数公式就可以进行转化和推导了：

      dx.ax = nVar * 9249h
            = nVar * -(10000h - 9249h)   // 一个数的补码再取负还是自身
                                         // 而这一步之后的9249h会被认为是无符号数
            = nVar * (9249h - 10000h)    // 消除外面的负号
            = 9249h*nVar - 10000h*nVar
    

  • 此时发现9249h被视为有符号数和nVar相乘的结果为9249h*nVar - 10000h*nVar（此时的9249h被视为了无符号），所以和我们想要的结果中多了一个-10000h*nVar，那么我们只要在结果中加上10000h*nVar得到9249h - 10000h*nVar + 10000h*nVar就是我们要的无符号数9249h和有符号数nVar相乘的“正确结果了”；而10000h超过了16位，10000h*nVar相当于将结果直接放到dx中

• 现在想要回到32位的场景中只需要把10000h扩展到100000000h，把9249h扩展到92492493h，把dx.ax扩展到edx.eax就可以了

• 再回头看上面的指令，执行完imul乘法后紧接着执行了一句add edx, ecx（ecx的值为nVar），那就相当于上面推导了将“错误”的结果再加上10000h*nVar就得到了“正确的结果”

• 所以add edx, ecx这一句的目的就是为了修正imul ecx这一条指令将92492493h当作有符号数处理的问题

现在再来分析最后面多的三条指令：

...               // 前面一大堆乘的结果保存在了edx.eax中，而直接拿edx使用相当于将结果右移32位
sar    edx, 2     // 在这里再次算术右移2位，相当于结果右移34为
mov    ecx, edx
shr    ecx, 1Fh   // 将结果逻辑右移31位，相当于将最高的符号位移动到了最低为，其他位清零；即正数结果为0，负数结果为1
add    edx, ecx   // 正数：结果加0，负数：结果加1

公式

最后三条指令的最终目的是正数结果不变，负数结果加1；这就是前面向零取整——正数向下取整、负数向上取整的公式：

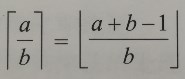
特征

...
mov    eax, imm
imul   reg
add    edx, reg
sar    edx, imm
mov    reg, edx
shr    reg, 1Fh
add    edx, reg
...

还原

不用在意修正的那条指令和后面根据符号位调整的三条指令，和前面无符号变量除正非2的幂的还原方式一样：m = 2^n / c => 2^n / m = c

nVar / 5

...
mov    ecx, [esp+0Ch+var_4]  // nVar_4 / 5
mov    eax, 66666667h
imul   ecx
[         ]                  // 这里比上面少一条
sar    edx, 1
mov    ecx, edx
shr    ecx, 1Fh
add    edx, ecx
...

指令分析

这里少的一句是修正的那句add edx, ecx，因为66666667h最高位为0，imul指令执行结果不会发生“错误”，所以就不需要这句了

特征

根据上面的特征，判断MagicNumber最高位不为0时就不需要那句add edx, reg了

nVar / 3

...
mov    ecx, [esp+0Ch+var_4]  // nVar_4 / 3
mov    eax, 55555556h
imul   ecx
[         ]                  // 这里又比上面少一条
mov    ecx, edx
shr    ecx, 1Fh
add    edx, ecx
...

指令分析

这里少的一句指令是sar edx, 1，这个实质上是直接使用了edx、原值右移32位刚刚够，所以不需要再次右移了

特征

这里的特征就需要再判断有没有那句shr edx, reg了，没有就是右移32位

8. 有符号数除负非2的幂

这种情况其实和上面有符号数除正非2的幂是相反的，而其相反的表现形式是MagicNumber要被视为负数

nVar / -3

...
mov    ecx, [esp+0Ch+nVar_4]  // nVar / -3
mov    eax, 55555555h
imul   ecx
sub    edx, ecx
sar    edx, 1
mov    ecx, edx
shr    ecx, 1Fh
add    edx, ecx
...

指令分析

前面提到这里的MagicNuber要被视为负数，而55555555h是个正数，所以就要将其修正为负数

nVar / -5

...
mov    ecx, [esp+14h+nVar_4]  // nVar / -5
mov    eax, 99999999h
imul   ecx
sar    edx, 1
mov    eax, edx
shr    eax, 1Fh
add    edx, eax
...

nVar / -7

...
mov    ecx, [esp+1Ch+nVar_4]  // nVar / -7
mov    eax, 6DB6DB6Dh
imul   ecx
sub    edx, ecx
sar    edx, 2
mov    ecx, edx
shr    ecx, 1Fh
add    edx, ecx
...